
第11回 何がその違いと関係しているのか〜基本的なデータ分析の読み方(2)
シティズンデータサイエンスラボは「AI技術を今役に立つ形で」を掲げる株式会社ソウジョウデータ(https://www.soujoudata.com/ )が運営する公式noteです。
他の説明変数が絡んだ関係
「p値」や「95%信頼区間」といったデータの見方を理解できれば「たまたまの差」に惑わされることはなくなります。それでもBIツールなどで描くグラフの多くは、1つの説明変数と1つのアウトカムの間の関係を2次元的にしか把握できません。立体的なグラフィックを使ったり、色分けをしたり、さまざまな手を尽くして複数の説明変数をグラフ上に同時に表示できる機能を持ったBIツールもありますが、今度は「ごちゃごちゃしてよくわからない」ものになりがちです。
また、「過去にクーポンつきのダイレクトメール(DM)を受け取ったことのある顧客はその後のリピート率が高い」というグラフが得られたとしても、即座に「もっとたくさんクーポンを送ってリピート率をあげよう!」というアクションを起こすべきとはなりません。なぜなら「特定の属性の顧客によくクーポンを送っている」という実態があるのだとすれば、その条件も考慮しなければならないからです。
たとえば、「首都圏在住の顧客には最近高い割合でクーポンを送っている」という事情があれば、顧客全体で「クーポンの有無別にリピート率を比較する」だけでなく、顧客全体を首都圏に住んでいるかいないかも分けた上で同様の集計を行なった結果を見ると、次のようなケースも考えられます。(図表2-7)

つまり、全体ではクーポンを受け取っていない人のリピート率は18.0%で、受け取っている場合は28.9%とこちらの方が高い結果になりますが、首都圏に住んでいればクーポンの有無にかかわらずどちらのリピート率も40.0%です。首都圏以外の地域に住む人もクーポンを受け取っていようがいまいが、同じく15.0%というリピート率を示しています。このような状況では「クーポンを送ればリピート率をあげられる!」とは考えにくいでしょう。単に、全体で見た「クーポンを受け取った顧客」のグループには相対的にリピート率の高い首都圏の顧客が含まれていただけ、と解釈する方が妥当です。BIツールのグラフだけを見て、焦ってクーポンを送っても、おそらくリピート率の向上は望めなかったでしょう。
このように、「何らかの説明変数の違いによって、アウトカムにどれだけ差があるか」を考えるためには、興味のある説明変数以外の条件をできるだけそろえなければいけません。この場合、首都圏に住んでいるかどうかで全体のデータをグループ分けしてから分析しましたが、このようなやり方を「サブグループ解析」と呼びます。
ただ、本書で考えてきたような、「活用のためのデータ」を用意すれば、ちょっとした業務のデータから、数百個以上もの説明変数を挙げることができます。これらの1つ1つを「サブグループ解析」して、確認するというのは現実的ではありません。数百項目を、ざっくり10個程度のサブグループに分けたとしても、数千枚のグラフを確認して、今回の例のように首都圏在住かどうか、という条件のような「サブグループ分けした時に差が消えるようなグラフはないか」と考えるのは不可能といっても過言ではありません。
サブグループ解析にかかる手間の膨大さを避ける多変量解析
「多変量解析」と呼ばれる統計学の手法を使えば、このようなサブグループ解析の手間を解決することができます。具体的には、アウトカムが売上などの数値であれば重回帰分析、アウトカムが「リピートするか離反するか」といったように2つに分かれるようなものであればロジスティック回帰分析といったものを用いることができます。
これらの手法は「横軸に1つの説明変数を考えて、縦軸にアウトカムを考えて」といった1対1の関係ではなく、「複数の説明変数とアウトカムの関係を一気に説明する」というものです。それぞれの説明変数とアウトカムの関係性は、「それ以外の説明変数の条件が一定だったとして」という条件の上で示されます。先ほどの、「首都圏に居住しているかどうか」と、「クーポンを受け取ったかどうか」という2つの説明変数を同時に使って、リピート率との関係を分析すると結果は次のようになります。(図表2-8)
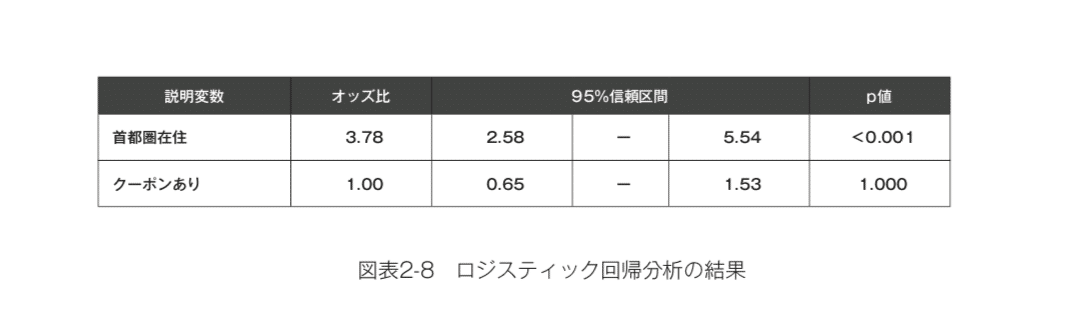
ロジスティック回帰分析の結果は「オッズ比」という指標で示されます。これが1より大きいということは「該当しやすい」、小さいということは逆に「該当しにくい」ということを示します。たとえば「首都圏に在住している」という説明変数の状態を取る場合、1より大きい3.78という値なので、首都圏在住の顧客はサブグループ解析で確認した際と同様に、「リピートしやすい」傾向にあるといえるでしょう。また、このオッズ比においても95%信頼区間とp値を考えることができます。分析する顧客の人数が少なければ、データのばらつきによって「たまたま差がつく」すなわち「たまたま1より大きなオッズ比が計算される」という可能性もなくはありませんが、95%信頼区間の値を見れば大まかにこのオッズ比は2.58~5.54という間にあると考えればよさそうです。したがってp値をみると、本来であれば首都圏在住者かどうかとリピート率に差がなかった場合に、たまたまこれほど(あるいはもっと強い)関連性が見られる確率は0.1%もないということがわかります。
しかし「首都圏在住かどうか」という条件をそろえた上で、「クーポンの有無がリピート率に関係するか」という結果をみると、そのオッズ比はちょうど1です。これはクーポンを受け取っていようがいまいが、リピート率が高いわけでも低いわけでもない、という結果を示しています。オッズ比が1というのは関連性の強さでいえば「全然関連していない」というもっとも弱い結果ですので、p値も1.000と、確率としてもっとも大きな値になります。
本マガジンは「統計学の教科書」ではありませんので、ロジスティック回帰の内容に興味のある方は拙著『統計学が最強の学問である 実践編』などを参照いただければ幸いですが、こうしたロジスティック回帰によって、サブグループ解析と同じように「首都圏在住者のリピート率は高い」「首都圏在住かどうかの条件をそろえるとクーポンの有無はまったく関係ない」という結果が得られることが理解いただけると思います。
ここから後は、説明変数が数百個になろうが、重回帰分析やロジスティック回帰分析といった手法を使えば大丈夫です。あたかもそれらすべての説明変数でサブグループ解析をやったかのように、「すべての説明変数の条件を互いにそろえ合った上で、それぞれの説明変数がどれほどアウトカムに関連しているか」を考えることができるでしょう。
ただし、考えた説明変数すべてを用いるべきかというとそういうわけではありません。今回の例の「クーポンを受け取ったかどうか」というように、まったくアウトカムと関係ない説明変数を考慮する必要はないでしょう。今回のように「まったく差がつかない」という場合ならまだしも、「まったく差がつかないはずなのに、たまたまちょっとだけ差がついてしまった」という状況が困りものです。「たまたまついた差」の影響を考慮して他の説明変数とアウトカムの関係性を考えても、それはあまり今後の役に立たないのです。次に同じデータを同じように分析したとして、この「たまたまついた差」は、もっと大きくなったり、小さくなったりと変化してしまうからです。
統計学はもちろんこうした事態に対処するための手法も発明しています。それはスパースモデリングという考え方です。この手法を使えば、同じロジスティック回帰分析や重回帰分析といった手法を使うにせよ、説明変数の候補がたくさんある中から、互いに条件をそろえる必要がある、アウトカムと明確な関係を持つような説明変数だけを使う組み合わせを自動的に考えることができます。このスパースモデリングの考え方はAIのための機械学習技術にも応用され、ディープラーニングを用いる中で、必要な項目だけを自動的に取捨選択することで、計算量を抑えつつ精度を向上させるという研究が存在しています。
実は本マガジンが、業務のためのデータから可能な限り多くの説明変数や特徴量の候補を考えよう、という立場なのは、スパースモデリングの存在によるところが大きいです。「仮説を考える」という頭の使い方によって人間の可能性を狭めるよりも、可能性を広げることに人間の頭を使った方が、人間とコンピュータとの作業分担としては賢明です。コンピュータはまだ「可能性を広げる」ことは得意ではありませんが、スパースモデリングを使えば「必要なものを自動的に取捨選択する」という作業は高速かつ正確に行なうことができます。
このようにして得られた分析結果をもとに、「解析単位の状態を変える」または「リソースの配分を変える」というアクションが取れれば、ビジネスの中で大きな価値を生むことになるでしょう。
