
第10回 何がその違いと関係しているのか〜基本的なデータ分析の読み方(1)
シティズンデータサイエンスラボは「AI技術を今役に立つ形で」を掲げる株式会社ソウジョウデータ(https://www.soujoudata.com/ )が運営する公式noteです。
効率的な「違いの見つけ方」
アウトカムと解析単位が決まり、データから考え得る限りさまざまな解析単位ごとの説明変数を加工することができたら、いよいよ分析に入りましょう。
再述しますが、データ分析のような定量的な研究は、「何かと何かの違いを生んでいる原因がどこにあるかを考える」ために行なわれます。したがって「購買金額の高い顧客とそうでない顧客の違い」のような、アウトカムがよい状態の解析単位と、そうでない解析単位の違いはどこにあるのか、と考えればよいわけです。
基本的な考え方としては、網羅的に考えられた説明変数のそれぞれと、アウトカムとの間に関連があるのかないのか、あるとすればどの程度の関連があるのかということを探していくことになります。ただし、BIツールやエクセルで片端から「説明変数を横軸に」「アウトカムを縦軸に」と集計すればよいというものではありません。このような考え方には大きく分けて3つの問題が存在しています。
①その関連性が「たまたまの差」なのかどうか判断できない
②複数の説明変数が絡んでくるような関連性について判断できない
③単純にとんでもない作業量がかかる
こうした問題を解決する便利な統計手法もすでに発明されているので最終的には心配する必要はありませんが、BIツールでの単純な集計で満足してしまわないよう、それぞれ見ていきましょう。
その差は「たまたまの差」なのか
たとえばあなたの会社で既存顧客の離反率に対して悩んでいたとしましょう。毎月、全体のうち約%もの顧客が離反してしまうため、新規顧客を獲得するコストはその後の売上によっても効率よくペイすることができません。そんな状況で、「離反してしまう顧客とそうでない顧客の違いはどこにあるか」と分析するのはとても合理的です。
そこであなたはBIツールを駆使し、さまざまな説明変数を横軸にした膨大な数のグラフを描画したところ、次に示すように「返金処理の経験がある顧客の離反率が高い」という結果が得られました。(図表2-2)

過去1か月間のデータを使って、それ以外の顧客では20%の離反率であるのに対し、返金処理の経験がある顧客では50%もの離反率が示されています。ここから、「返金処理の対応に何か不満を持たれているのではないか」とか、「そもそも返金を頼みたくなるような商品とは何だったのか」という侃々諤々の議論もできますが、その前にするべきことがあります。
それは、「たまたまの差」なのではないかと考えることです。これが、全体で102人のデータで、そのうち返金処理の経験者が1人しかいなかったとすればどうでしょうか?2人中1人がたまたま離反していただけなら、「たまたま」という気もします。返金経験者が2人しかいないのならば、得られる割合は0%、50%、100%のいずれかの値にしかなりません。20%ちょうどという値にならない以上、たまたま2人とも離反してなければ「なぜか離反率が低い!」というグラフが見えていたでしょう。
しかし、100万人の顧客のうち20万人が返金処理をしていた、という状況ではどうでしょうか?つまり、返金処理を経験していない80万人中の20%で16万人が離反し、経験している20万人中その半分の10万人が離反している、という状況です。さすがに何万人もの顧客が「たまたま」離反しているとは考えにくいはずです。
このように、単純に割合や平均値を集計して比較しただけでは、「たまたまの差」かどうかという判断ができません。統計学では「p値」という「本来まったく差がなかった状態で、このような(あるいはそれ以上に差がつく)分析結果が得られる確率はどれほどあるのか」を考えます。この確率が低くければ「たまたまとは言い難い」と考えられますし、高ければ「たまたまという可能性が捨てきれないからあまり気にしない方がいい」と考えられます。
実際に両者のケースについて「p値」を計算してみると次のようになります。(図表2-3、2-4)

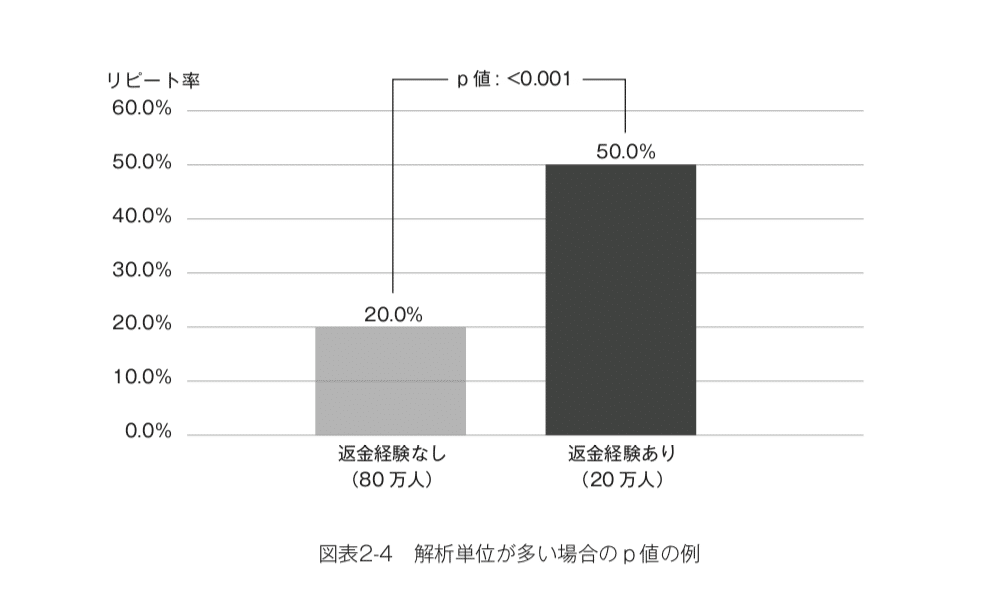
つまり、102人中2人の返金経験者だけで50%という高い離反率が出た、という程度の差はまったくの偶然でも0.299という高い確率で得られるということです。「3割バッターがヒットを打った」といわれても誰も驚かないのと同様に、この値がまったくの「たまたま」で得られたといわれても否定することはできません。一方で、100万人中20万人の返金経験者がこれほど高い離反率を示すという結果が「たまたま」得られる確率は0.1%もありません。そのような奇跡が起こっただけです、という説明にはムリがあります。
統計学では、両者の間に差があるのかどうか、という仮説を検証するためにp値を計算する仮説検定を行ないます。なお、慣例的には5%未満すなわち「20回に1回も得られない」ような結果が出れば、その差は「たまたま」とは考えにくいクリアなものだと考えます。
ただし、数十万人同士で比べれば、かなり小さな差であっても「たまたま」とはいい難いという結果が得られることもあります。たとえば同じように100万人中20万人の返金経験者のうち、ちょうど21%(4.2万人)が離反していて、残り80万人の非経験者では20%(16万人)が離反していたとしましょう。わずか1%ポイントの差しかないため、実用上はあまり気にならないかもしれません。しかし、仮に両グループの間にまったく差がなかったのだとすれば「たまたま返金経験者にこれほど離反者が偏る」確率はとても低く、p値はやはり0.1%未満です。
したがってp値で「たまたまの差かどうか」を判断するだけではなく、「たまたまのバラツキなどを考慮した上で、だいたいどの程度の差なのか」を確認した方がよい場合もあります。「95%信頼区間」という指標を使えば、次図のように、いくつからいくつまでの値だと考えるのが妥当かという目安を示せます。今回の状況であればこの1%ポイントの差はたまたまのバラツキなどを考慮すると「おおむね0.8〜1.2ポイントと考えるのが妥当」と判断できます。(図表2-5)

なお、同様に先ほどの「20万人の返金経験者のうち10万人が離反」といった状況に対する95%信頼区間を示すと、「返金経験者の方が29.8〜30.2ポイントも離反率が高い」という結果になります。(図表2-6)

「たまたまの差」であれば、そこからのアクションはムダになってしまうかもしれませんが、統計学の見方を身につければ、そうしたリスクは回避できます。また第一章で「ごくわずかの解析単位しか該当しない」分け方は避けるべきだと述べましたが、それは、多少アウトカムに差がつこうとも、「p値が大きくてたまたまという可能性が捨てきれない」という結果にしかならないためであることが、改めて理解してもらえたのではないでしょうか。
